При исследованиях общих закономерностей сложного поведения нелинейных систем особое внимание привлекают коллективные явления в ансамблях связанных элементов. Здесь интересны системы, в которых собственная динамика элементов ансамбля проста, а сложность возникает как следствие их сетевого взаимодействия. С точки зрения вопросов управления и самоорганизации важны ситуации, когда коллективные явления возникают именно при слабой связи между элементами или несильном воздействии на них.
По этим причинам в центре внимания оказываются ансамбли осцилляторов, которые в отсутствии связи находились бы в устойчивом режиме периодических колебаний. В самом деле, если элементы находятся в устойчивом стационарном состоянии, слабое воздействие лишь несущественно сдвинет положение равновесия каждого элемента, но не вызовет нетривиальных коллективных явлений. Если, напротив, собственная динамика элементов хаотична, сложность в поведении системы будет присутствовать изначально, без связи, — и это предмет отдельного направления исследований. В системах с периодическими же колебаниями собственная динамика проста, но есть одна нейтрально устойчивая степень свободы — фаза колебания — и слабое воздействие на систему может позволить управлять динамикой этой фазы, добиваясь совпадения ритмов колебаний элементов. Оказываются возможны коллективные явления при слабых связи или воздействии. С практической точки зрения, именно примерами связанных периодических осцилляторов являются электродвигатели и роторные двигатели, смонтированные на общей платформе, массивы одинаковых электроприборов, подключенных к общей сети переменного тока, пешеходы на мосту, колонии бактерий, и т.д.
В основе математической теории коллективных явлений в таких системах лежит фазовое описание, при котором главное внимание уделяется динамике фазы колебания элемента. Математически, на уровне уравнений, исследуется динамика ансамблей фаз. В течение последних 20 лет было обнаружено, что при наличии некоторого свойства фазового ансамбля, его коллективная динамика приобретает очень специфический вид. В ансамбле N элементов независимыми являются три переменных, две из которых связаны с параметром порядка (мерой синхронности элементов ансамбля), и имеется N-3 интеграла движения. Причем это справедливо при любом значении N, для сколь угодно больших ансамблей. Систематически данные результаты оформились в виде теорий Ватанабэ-Строгаца и Отта-Антонсена. Наиболее существенно здесь то, что большая часть парадигматических моделей фазовых ансамблей, на исследовании которых исторически происходило становление теории коллективных явлений в ансамблях осцилляторов, оказываются обладающими этим свойством. Таким образом, появился инструмент, позволяющий далеко продвинуться в описании и понимании динамики парадигматических моделей. Но одновременно оказалось, что эти модели являются специфическими и требуется анализ, насколько полученные для них результаты справедливы применительно к реальным системам, для которых условия теории Отта-Антонсена будут выполняться приблизительно.
С точки зрения математической физики, ответ на последний вопрос требует построение теории возмущений для подхода Отта-Антонсена. Такая теория возмущений давала бы информацию о том, как нарушение свойств Отта-Антонсена сказывается на коллективной динамике в ансамблях. Попытки построения такой теории многие годы сталкивалась с трудностями в силу объективных причин — существенной вырожденности математических свойств базовой теории. (В теоретической физике можно привести пример подобной ситуации: в кинетической теории газов вычисление транспортных коэффициентов — теплопроводности, диффузии и т.д. — на основе кинетического уравнения Больцмана не является техническим упражнением на использование метода многих масштабов, а потребовало построения особой математической теории Чепмена-Энскога.)
В недавней статье сотрудников и студентки кафедры теоретической физики ПГНИУ в ведущем физическом журнале Phys. Rev. Lett. (Impact factor 2016: 8.462)
I.V. Tyulkina, D.S. Goldobin, L.S. Klimenko, and A. Pikovsky, “Dynamics of Noisy Oscillator Populations beyond the Ott-Antonsen Ansatz”
предложена смена парадигмы — вводятся “круговые кумулянты”, в терминах которых описывается коллективная динамика ансамблей. В рамках “кумулянтного подхода” удаётся изучить влияние внутреннего шума на динамику ансамблей. Есть основания полагать, что новый подход позволит построить общую теорию возмущений для подхода Отта-Антонсена; на данный момент в рамках подхода уже получены результаты для ряда ситуаций, которые ранее не поддавались исследованию (статья в Phys. Rev. Lett. представляет часть этих результатов).
Синхронное вспыхивание колонии светлячков
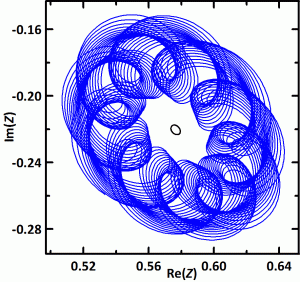
Пример траектории параметра порядка в ансамбле с иерархией связей между элементами
P.S. Сразу после публикации на сайте Phys. Rev. Lett. статья была отмечена в twitter’е Стивеном Строгацем (Steven Strogatz — американский математик и физик, один из классиков в теории хаоса и самоорганизации, писатель, популяризатор науки), за чем последовали ретвиты исслелдователями из разных стран и двумя научными сообществами в США. Верхняя оценка суммарной аудитории твит-каналов, опубликовавших новость о статье: 64.5 тыс. подписчиков.